Simpler tactics could be considered ways to redistribute the load in favor of stronger partners in the position of the weakest rivals. However, if the match load of his team is distributed in favor of the strongest, it will inevitably lead to a drop in their ratings below the level of the rest of the team. Hence, it is necessary to distribute before equiparametric comparison of ratings (ER (Rt)). However, this does not exhaust the task. After all, there is still a factor of exchange – strong and weak partners, rivals. In order to achieve the greatest effect in it, it is necessary to find the equiparametric efficiency distribution (ER (E)) in the form of load distribution δijl for every possible exchange.
Denote – the effectiveness and rating of the team as a whole; Δij – the share of the load (martial arts) for the exchange i (with Rti) against j (with Rtj) from the common one; Δрр – average load for each exchange.
Δigra = Δ average difference in ratings + Δ effective use

Teamwork of this player with a partner can be characterized as a difference in the effectiveness of his game in the presence of this partner on the field and in his absence. Similarly, one can characterize the expediency of entering this player’s field when the player of the rival team is on the field. From the players of his team, those who have the greatest total balance of teamwork, both on the partners, and on countering the opponents on the field are used. Effectiveness values during the meeting:
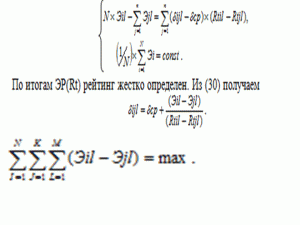

Teamwork of this player with a partner can be characterized as a difference in the effectiveness of his game in the presence of this partner on the field and in his absence. Similarly, one can characterize the expediency of entering this player’s field when the player of the rival team is on the field. From the players of his team, those who have the greatest total balance of teamwork, both on the partners, and on countering the opponents on the field are used. Effectiveness values during the meeting:
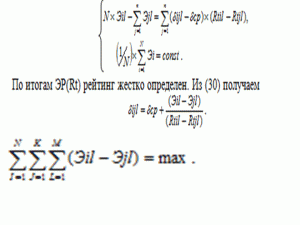




 06.04.2017
06.04.2017






