Sport is a struggle for results. If the understanding of the result is the difference between the scored (Z) and the missed (P) balls (realized actions), then the game’s meaning is to create a positive difference. Participants can be arranged in descending order of the difference they create in a duel with a virtual average rival. The difference in their ratings corresponds to the actual outcome of a personal meeting. The rating model should ensure this convergence. To do this, you should represent the participant’s rating as its result in a one-year macro tournament, which in real life consists of a set of micro tournaments.
All who are engaged in this sport in Holland, France, Russia, Georgia, the United States and other countries have played each with each. Tournament in the scale of one country, division into weight categories – these are all examples of the prototype of the macro tournament. A macro tournament is a hypothetical concept. It is impossible to realize it in a circular system. We use the principle of transitivity – if A has played better B all season, and B – better C, then A will be higher in the final rating list, and B, and C. In this case, why should A play with C?
From the current results of its participant determine the level of the game, according to which it is easy to predict the results of the macro-tournament that have not been played. Although there is always Thomas the Unbeliever, who wants to play and check the convergence of actual and predicted results.
The determining function in the convergence of the model is the kind of rating functional dependence. It is the search for the function with the greatest convergence in different sports is the most time consuming. As a result, it was possible, though not much, to bypass the well-known table of Elo coefficients in this.
Convergence also depends on the form of the recount. If we write a formula for one participant, then another, third, then we successively write out a system of linear equations that has or does not have a solution. Many calculation schemes (Elo, tennis classifications) provide themselves with relative spontaneous convergence due to a safety net from the system of equations actually received. For clarity, consider a few examples.
Consider an example of checkers. Suppose that you have had 10 meetings in the tournament. If any of the opponents do not have a rating, then they assign an average value of 2200. Average rating of your opponents, let 2500. You won 7: 3. Your rating for this tournament will be:
.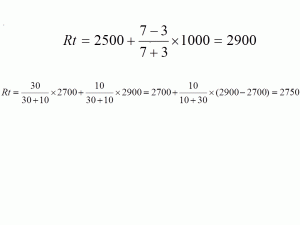
But this rating in this particular tournament. And in general for the season you have already played 30 matches. And received, say, 2700. Then your seasonal rating:
Let your team play some games in hockey. The sum of the goals scored and missed in the previous meetings of the season is 30, the seasonal rating is 2700. You won the next meeting 7: 3 from the opponent with a rating of 2500. After this meeting, the seasonal rating of your team changed completely similarly.
Suppose you are engaged in boxing, did not consider the seasonal rating, but now suddenly you wanted to do it. You have fought three fights with a boxer whose rating is currently 2500, two fights with a boxer who has a rating of 2420 and only one fight against a boxer with a rating of 2300. The total score for all six meetings determined by the judges is 30:20. You were confronted by a virtual boxer, 3/6 consisting of a rating of 2500, 2/6 boxing at 2420 and 1/6 – 2300. The strength of this generalized virtual opponent is
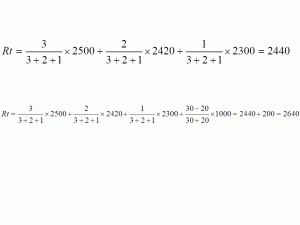
You are stronger than this virtual opponent by 200 points
This is how the participants of the competition will count. Organizers better create a program that will solve the SLP with a typical equation like the last example and publish the results on the Internet daily. The system is transparent. Any participant at any time can easily check the organizers, creating his own equation like the last example and checking his calculated rating with official data. There is no need for inventing arbitrarily corrected coefficients, which improves the quality of the model.
In boxing, you can distinguish between battles at the far, middle and short distances.These are already private components. If the boxer has a common ratio of 30:20, distributed according to the distance of the battle – 10: 2, 10:10, 10: 8, then from this it is clear that the fight at long range is clearly preferable. Convergence of general and partial sums ensures continuity of general and private ratings. They are considered similar. With the only difference is that the accumulation of information to the athlete or his coach will have to do on their own.
It is mathematically proven that there is no difference in the results if you decide on the whole macro-tournament as a whole, or calculate the SLP in each tournament (component), combining the results obtained in proportion to their specific gravity.Considering the private ratings of their rivals, you can calculate in them the ratio of the strikes of the meeting that has not yet taken place and make adjustments. In the fight, the capture, throw and hold are similarly arranged. You can also find out who is the champion, for example, in the chess Sicilian defense.
В игровых видах спорта рейтинг команды аналогично раскладывается сначала по игрокам, а потом еще и по компонентам. Разница в рейтингах игроков А и Б соответствует разнице в счете команд, состоящих только из игроков А и только игроков Б.
Результативность большинства видов спорта имеет тенденцию к сокращению. Первый финальный матч чемпионата мира по футболу закончился со счетом 8:3. В наше время нулевые счета матчей в футболе стали нормой. Аналогична ситуация в боксе. С начала столетия на Олимпийских играх число ударов, фиксируемых судьями в боксе, сократилось вдвое. Как отреагирует на такое изменение рейтинг? Одним из способов можно рассматривать анализ количества активных действий – ударов. Если соотношение ударов не меняется, то на рейтинг никакого влияния это изменение не будет. Другое дело, что цена одного удара возрастает.
Handbook of Ratings. Approaches to Ratings in the Economy, Sports, and Society / A. Karminsky. A. Polozov/ International Publishing house “Springer”, 2016., 360c.




 06.05.2017
06.05.2017






